Home
Up
 

CONTROLLABILITY: 

If a system is described by the equation

[dx/dt] = [A][x] + [B][u] (where A, B) are matrices

Then the system is said to be controllable if 

rank [B  AB A²B ... A^n-1B] = n

Therefore for a Single-Input-Single-Output [SISO] system the controllability matrix P_c is given by

P_c = [B  AB A²B ... A^n-1B]

 If the determinant of P_c  is nonzero the system is controllable

OBSERVABILITY:

The roots of the characteristic equation can be placed where desired in the s-plane if, and only if, a system is observable and controllable!

If a system is described by the equations

[dx/dt] = [A][x] + [B][u] and [y] = [C][x] (where A, B, C) are matrices then the observability matrix Qo is defined as

Q_o = [B  AB A²B ... A^n-1B]^T

Then the system is observable if the determinant of Q_o  is nonzero!

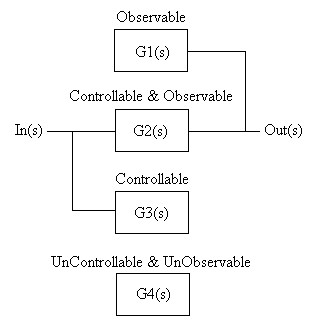
The figure below shows the notional concepts of controllable, observable, uncontrollable and unobservable.