y (t) = 1 - (e^{--z*ω*t)*Sin( ω*√(1 - z*z)*t +Arc Cos(z) ) / √(1 - z*z)}

	z = 0.1 =  low damped system many oscillations in (green) output
	z = 1 =  high damped system no oscillations in (purple) output

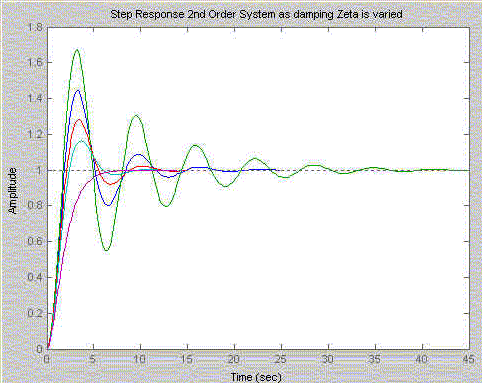
What does changing the value of  z mean with respect to the pole positions of the system. As the value of damping z decreases the position of the pole approaches the imaginary axis. 

	The concentric circles represent a constant frequency as damping is varied.
	The radial lines represent constant damping as frequency is varied

Transient Response (time domain) of systems to a step disturbance:

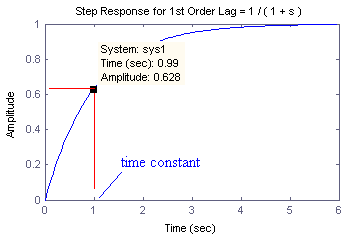
A first order system - the time constant of the system is calculated by reading off the time where the output reaches 63% of its final value.

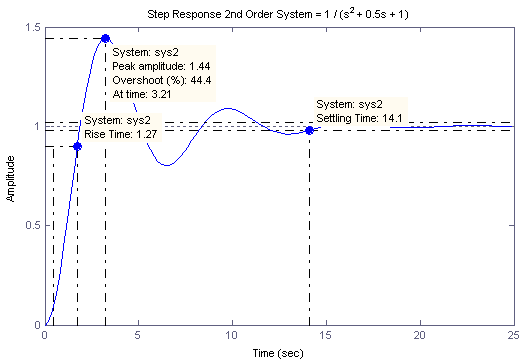
For a second order system several parameters are used to specify the response characteristics:

	Rise Time: the time difference between 10% and 90% output amplitude values
	Peak Amplitude: the magnitude of the maximum overshoot seen in the response usually given as a % or a gain in dB
	Settling Time: the time for the output amplitude to remain within some predefined tolerance limits typically these limits are +/- 2%, 5%, 10% of the steady state value

Calculations used for time response characteristics:

 

	ωn = ωo	natural frequency
	Note:	ωn = 2*π*fn		Rise time	Peak Time
				(p - b)/ωd
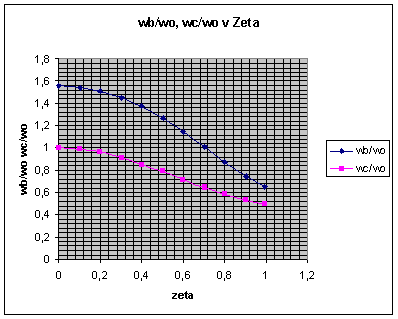
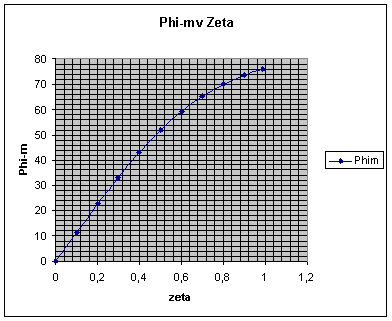
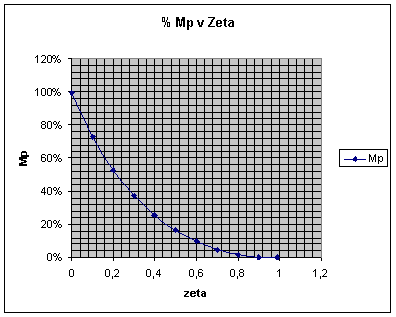
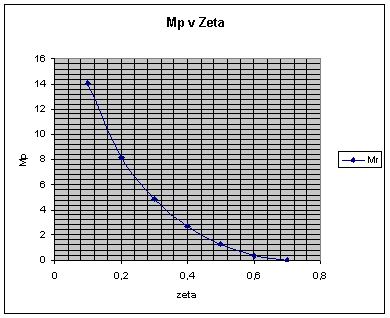
ζ	damped frequency ωd	b	σ	Tr	Tp	Mp = M	Ts 2%	Ts 5%	Mr = Mp	ωr	ωb	ωc	ωo*Tr	ωb/ωo	ωc/ωo	Φm
	[Hz]	arctan(ωd/σ)	ζ*ωn	[s]	[s]	%	[s]	[s]	[dB]	[Hz]	[Hz]	[Hz]				deg
0.001	1	1.569796327	0.001	1.5718	3.1416	100%	4000	3000	53.9794	1	1.5538	1	1.5718	1.5538	1	0.11581
0.1	0.99499	1.470628906	0.1	1.67938	3.1574	73%	40	30	14.02305	0.98995	1.5428	0.9901	1.67938	1.5428	0.9901	11.4217
0.2	0.9798	1.369438406	0.2	1.8087	3.2064	53%	20	15	8.136088	0.95917	1.5096	0.9608	1.8087	1.5096	0.9608	22.6032
0.3	0.95394	1.266103673	0.3	1.96605	3.2933	37%	13.333	10	4.846561	0.90554	1.4537	0.9144	1.96605	1.4537	0.9144	33.2733
0.4	0.91652	1.159279481	0.4	2.16288	3.4278	25%	10	7.5	2.695407	0.82462	1.3745	0.8544	2.16288	1.3745	0.8544	43.1182
0.5	0.86603	1.047197551	0.5	2.4184	3.6276	16%	8	6	1.249387	0.70711	1.272	0.7862	2.4184	1.272	0.7862	51.8278
0.6	0.8	0.927295218	0.6	2.76787	3.927	9%	6.6667	5	0.354575	0.52915	1.1482	0.7157	2.76787	1.1482	0.7157	59.1877
0.7	0.71414	0.79539883	0.7	3.28533	4.3991	5%	5.7143	4.2857	0.001738	0.14142	1.01	0.6482	3.28533	1.01	0.6482	65.1567
0.8	0.6	0.643501109	0.8	4.16349	5.236	2%	5	3.75	0.354575	#NUM!	0.8709	0.5868	4.16349	0.8709	0.5868	69.8603
0.9	0.43589	0.451026812	0.9	6.17258	7.2073	0%	4.4444	3.3333	2.107014	#NUM!	0.7461	0.5327	6.17258	0.7461	0.5327	73.5139
0.999	0.14107	0.141539473	0.99	21.2668	22.27	0%	4.0404	3.0303	11.07817	#NUM!	0.6528	0.4902	21.2668	0.6528	0.4902	76.0935