Home
Up
 

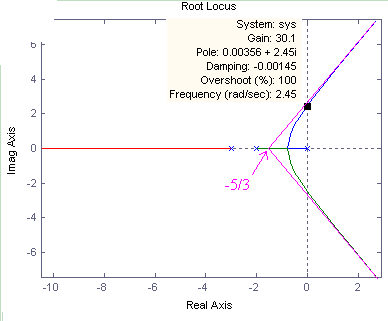
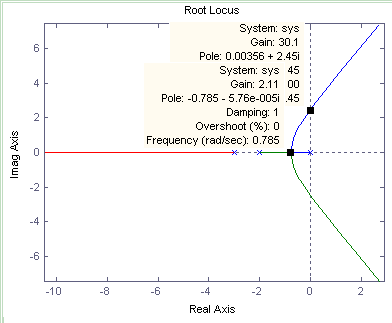
ROOT LOCUS:

Used on the open loop system transfer function to calculate closed loop response:

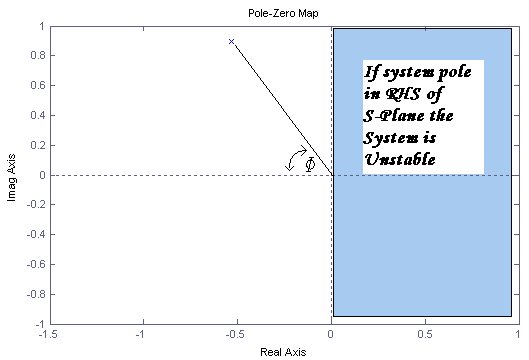
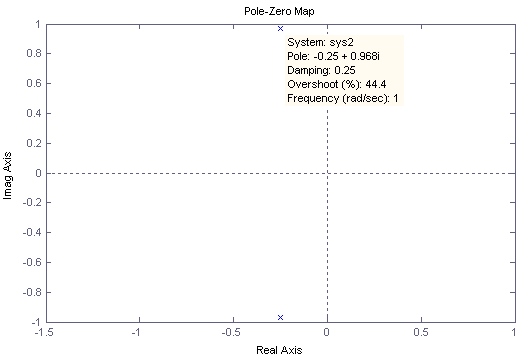
When f = 0 deg,  z = 1 and when f = 90 deg,  z = 0 using the equation z = Cos (f)

Basic Steps to Obtain The Root Locus of a closed loop control system

  1. Step
    bulletFind the characteristic equation and arrange it to be in the form
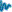    bulletP(s) + K*Q(s) = 0
    bulletP(s) represents the poles and Q(s) represents the zeros
  2. Step
    bulletfactor P(s),Q
    bullet(s + a1)...(s + an) + K*(s + b1)...(s + bn) = 0
  3. Step
    bulletDraw the position of the poles and zeros on the s-plane
  4. Step
    bulletLocate the segments of the real axis that are parts of the root locii using the rule
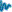    bulletThe root locus on the real axis always lies to the left of an odd number of poles
  5. Step
    bulletFind how many separate locii and asymptotes there are using the rule
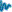    bulletThe number of separate locii is equal to the number of poles
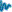    bulletThe number of asymptotes  = Number of Poles - Number of Zeros
  6. Step
    bulletNote that root locii are symmetrical about the horizontal real axis
  7. Step
    bulletLocii proceed to the zeros at infinity along asymptotes centred at sa with angles fa the asymptotes are centred at a point on the real axis given by:
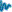    bulletsa = S poles of P(s) - S zeros of P(s) / (npoles - nzeros)
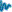    bulletfa = (2q + 1)*180º/(npoles - nzeros)  where q = 0,1,...
  8. Step
    bulletFind the point where the locus crosses the imaginary axis by using the Routh-Hurwitz criterion
  9. Step
    bulletFind the breakaway point, if any, on the real axis, note that the tangents to the breakaway point are equally spaced over 360º
  10. Step
    bulletFind the angle of departure of the locus from a pole and the angle of arrival of the locus at a zero. Use the fact that
  11. Step
    bulletFind the root locations that satisfy the phase criterion at the root sj where j = 1,2, ...,npoles

    EXAMPLE

    The Characteristic Equation is given as:
    bullets(s + 2)(s + 3) + K = 0
    bullet# of poles n = 3
    bullet# of zeros m = 0
    bullet# of asymptotes = n – m = 3
    bulletn – m is odd therefore one asymptote is on the negative real axis
    bulletAngle between asymptotes is given by 360º/(n-m) = 360º/(3 – 0) = 120º
    bulletThe asymptotes meet at point given by
    bulletsasymReal = (Σ (real parts of poles) - Σ (real parts of zeros) )/(n-m)
    bulletsasymReal = ((0 +(-2)+(-3)) – (0))/3 = -5/3
    bullet ffind the intersection of locus with Imaginary axis, we use the characteristic
    bulletequation and substitute jω for s
    bullets(s+2)(s+3) + K = 0
    bullets3 + 5s2 + 6s + K = 0
    bulletjω3 - 5ω2 + 6jω + K = 0
    bulletEquate Real and Imaginary Parts to 0
    bulletWhen Real Part = K - 5ω2 = 0
    bulletWhen Imaginary Part = 6jω - jω3 = 0
    bulletUsing the above equations we find two sets of solutions
    bulletK = 0 and ω = 0
    bulletK = 30 and ω = ±√6
    bulletWe can also use Routh’s Stability Criterion on the Characteristic Equation to find Imaginary axis intersection
    bulletCalculate Breakaway Point using the characteristic equation
    bullets(s+2)(s+3) + K = (s+a)2(s+b)
    bullets3 + 5s2 + 6s + K = (s2 + 2as a2)(s+b)
    bulletLHS = RHS of equation.
    bulletRHS = s3 +(2a+b)s2+(a2+2ab)s+a2b
    bulletEquating coefficients with LHS gives
    bullet2a + b = 5
    bullet2a + 2ab = 6
    bulletK = 2ab
    bulletWe can solve these equations and obtain the following:
    bulleta = (5 ±√7)/3, b = (5 ±2√7)/3, K = 2.1126